Koko loves to eat bananas. There are n piles of bananas, the ith pile has piles[i] bananas. The guards have gone and will come back in h hours.

Koko can decide her bananas-per-hour eating speed of k. Each hour, she chooses some pile of bananas and eats k bananas from that pile. If the pile has less than k bananas, she eats all of them instead and will not eat any more bananas during this hour.

Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.

Return the minimum integer k such that she can eat all the bananas within h hours.

Example 1:
Input: piles = [3,6,7,11], h = 8
Output: 4

Example 2:
Input: piles = [30,11,23,4,20], h = 5
Output: 30

Example 3:
Input: piles = [30,11,23,4,20], h = 6
Output: 23

Constraints:

• 1 <= piles.length <= 104
• piles.length <= h <= 109
• 1 <= piles[i] <= 109

We want to apply the binary search template, and implement the feasible function. Here, the feasible function is whether Koko can_finish_eating all piles within h hours while eating at speed k per hour.

Since Koko eats at only one pile during each hour, ceil(float(p)/k) is the time Koko takes to finish pile p. Note that p/k does not work here because we want a whole number of hours so we needed to round up p/k. Therefore, the feasiblity is determined by whether Koko's hours_used is within h hours, where hours_used is the total hours to finish all piles.

Recall example 1 with Input: piles = [3,6,7,11], h = 8, and Output: 4, the can_finish_eating function returns the following results.

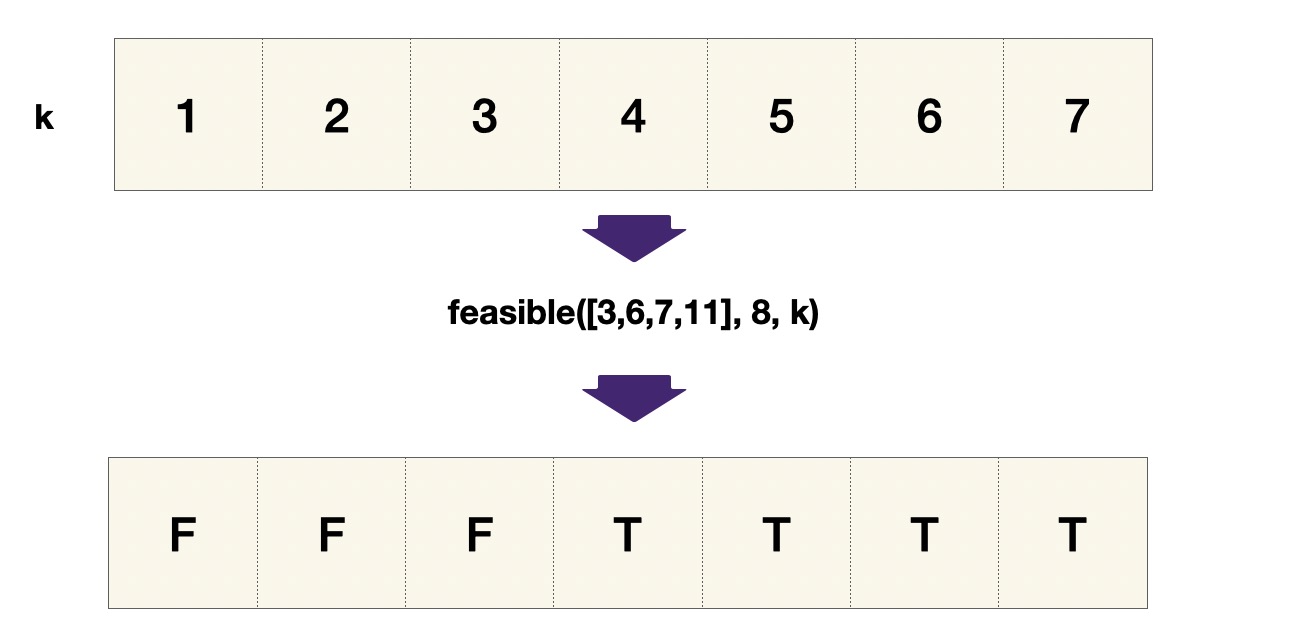
Implementation

def can_finish_eating(piles, h, k):
    hours_used = 0
    for p in piles:
        hours_used += ceil(float(p)/k)
    return hours_used <= h

def minEatingSpeed(piles, h):
    left, right = 1, 1000000000 # 10^9 max length of the piles
    ans = -1
    while left <= right:
      mid = (left + right) // 2
      if can_finish_eating(piles, h, mid):
          ans = mid
          right = mid - 1
      else:
          left = mid + 1
    return ans