Pacific Atlantic Water Flow
There is an m x n rectangular island that borders both the Pacific Ocean and Atlantic Ocean. The Pacific Ocean touches the island's left and top edges, and the Atlantic Ocean touches the island's right and bottom edges.
The island is partitioned into a grid of square cells. You are given an m x n integer matrix heights where heights[r][c] represents the height above sea level of the cell at coordinate (r, c).
The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell's height is less than or equal to the current cell's height. Water can flow from any cell adjacent to an ocean into the ocean.
Return a 2D list of grid coordinates result where result[i] = [ri, ci] denotes that rain water can flow from cell (ri, ci) to both the Pacific and Atlantic oceans.
Example 1:
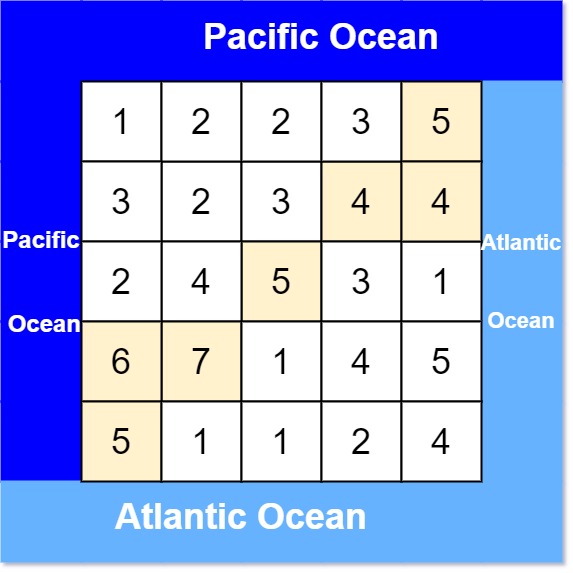
Input: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
Explanation: The following cells can flow to the Pacific and Atlantic oceans, as shown below:\
[0,4]: [0,4] -> Pacific Ocean [0,4] -> Atlantic Ocean [1,3]: [1,3] -> [0,3] -> Pacific Ocean [1,3] -> [1,4] -> Atlantic Ocean [1,4]: [1,4] -> [1,3] -> [0,3] -> Pacific Ocean [1,4] -> Atlantic Ocean [2,2]: [2,2] -> [1,2] -> [0,2] -> Pacific Ocean [2,2] -> [2,3] -> [2,4] -> Atlantic Ocean [3,0]: [3,0] -> Pacific Ocean [3,0] -> [4,0] -> Atlantic Ocean [3,1]: [3,1] -> [3,0] -> Pacific Ocean [3,1] -> [4,1] -> Atlantic Ocean [4,0]: [4,0] -> Pacific Ocean [4,0] -> Atlantic Ocean
Note that there are other possible paths for these cells to flow to the Pacific and Atlantic oceans.
Example 2:
Input: heights = [[1]]
Output: [[0,0]]
Explanation: The water can flow from the only cell to the Pacific and Atlantic oceans.
Constraints:
m == heights.lengthn == heights[r].length1 <= m, n <= 2000 <= heights[r][c] <= 105
Solution
The best way to approach this question is to traverse from the outside cells into the inner cells. Both BFS and DFS will produce an efficient implementation. Below, we will to show a recusive dfs approach to this problem. To find the cells that will flow to both oceans, we will recursively find the cells that can be reached by the Pacific Ocean, and the cells reached by the Atlantic Ocean. Finally, we find the overlapping cells that can be reached by both oceans.
Implementation
def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
m = len(heights)
n = len(heights[0])
pacific = [[False for _ in range(n)] for _ in range(m)]
atlantic = [[False for _ in range(n)] for _ in range(m)]
res = []
dirs = [(0,1), (0,-1), (1,0), (-1,0)]
def get_neighbours(x, y):
neighbours = []
for dirx, diry in dirs:
newx, newy = x+dirx, y+diry
if 0 <= newx < m and 0 <= newy < n:
neighbours.append((newx, newy))
return neighbours
def dfs(x, y, ocean):
if ocean[x][y]: return
ocean[x][y] = True
for newx, newy in get_neighbours(x,y):
if heights[newx][newy] >= heights[x][y]:
dfs(newx, newy, ocean)
for x in range(m):
dfs(x, 0, pacific)
dfs(x, n-1, atlantic)
for y in range(n):
dfs(0, y, pacific)
dfs(m-1, y, atlantic)
for x in range(m):
for y in range(n):
if pacific[x][y] and atlantic[x][y]:
res.append([x,y])
return res
Ready to land your dream job?
Unlock your dream job with a 2-minute evaluator for a personalized learning plan!
Start EvaluatorWhich technique can we use to find the middle of a linked list?
Recommended Readings
LeetCode Patterns Your Personal Dijkstra's Algorithm to Landing Your Dream Job The goal of AlgoMonster is to help you get a job in the shortest amount of time possible in a data driven way We compiled datasets of tech interview problems and broke them down by patterns This way we
Recursion Recursion is one of the most important concepts in computer science Simply speaking recursion is the process of a function calling itself Using a real life analogy imagine a scenario where you invite your friends to lunch https algomonster s3 us east 2 amazonaws com recursion jpg You first
Runtime Overview When learning about algorithms and data structures you'll frequently encounter the term time complexity This concept is fundamental in computer science and offers insights into how long an algorithm takes to complete given a certain input size What is Time Complexity Time complexity represents the amount of time
Want a Structured Path to Master System Design Too? Don’t Miss This!