Redundant Connection
In this problem, a tree is an undirected graph that is connected and has no cycles.
You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.
Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.
Example 1:
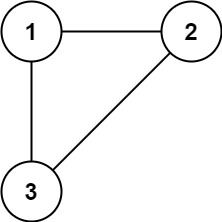
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]
Example 2:
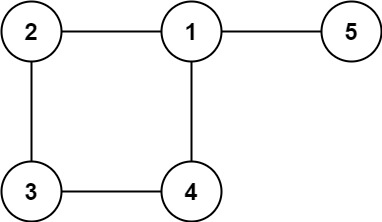
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]
Constraints:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ai < bi <= edges.lengthai != bi- There are no repeated edges.
- The given graph is connected.
Solution
We will apply Kruskal's algorithm using Union Find on this special graph where all the edges have equal weight (no sorting needed!).
Instead of discarding an edge when we find a cycle, we return this edge as the answer.
Moreover, the weight of the path is irrelevent to the problem, so we will not keep track.
We follow the same implementation as finding the minimum spanning tree using Kruskal's algorithm.
When we find an edge e such that its two ends are in the same component, we know that it will create a cycle, hence e is the extra edge added into the tree.
Implementation
def findRedundantConnection(edges: List[List[int]]) -> List[int]:
id = {}
def find(x):
y = id.get(x, x)
if y != x:
id[x] = y = find(y)
return y
def union(x, y):
id[find(x)] = find(y)
for e in edges:
if find(e[0]) == find(e[1]): # two ends in the same component
return e
union(e[0], e[1]) # join two components
Ready to land your dream job?
Unlock your dream job with a 2-minute evaluator for a personalized learning plan!
Start EvaluatorThe three-steps of Depth First Search are:
- Identify states;
- Draw the state-space tree;
- DFS on the state-space tree.
Recommended Readings
LeetCode Patterns Your Personal Dijkstra's Algorithm to Landing Your Dream Job The goal of AlgoMonster is to help you get a job in the shortest amount of time possible in a data driven way We compiled datasets of tech interview problems and broke them down by patterns This way we
Recursion Recursion is one of the most important concepts in computer science Simply speaking recursion is the process of a function calling itself Using a real life analogy imagine a scenario where you invite your friends to lunch https algomonster s3 us east 2 amazonaws com recursion jpg You first
Runtime Overview When learning about algorithms and data structures you'll frequently encounter the term time complexity This concept is fundamental in computer science and offers insights into how long an algorithm takes to complete given a certain input size What is Time Complexity Time complexity represents the amount of time
Want a Structured Path to Master System Design Too? Don’t Miss This!