Rotting Oranges
You are given an m x n grid where each cell can have one of three values:
0representing an empty cell,1representing a fresh orange, or2representing a rotten orange.
Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.
Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.
Example 1:
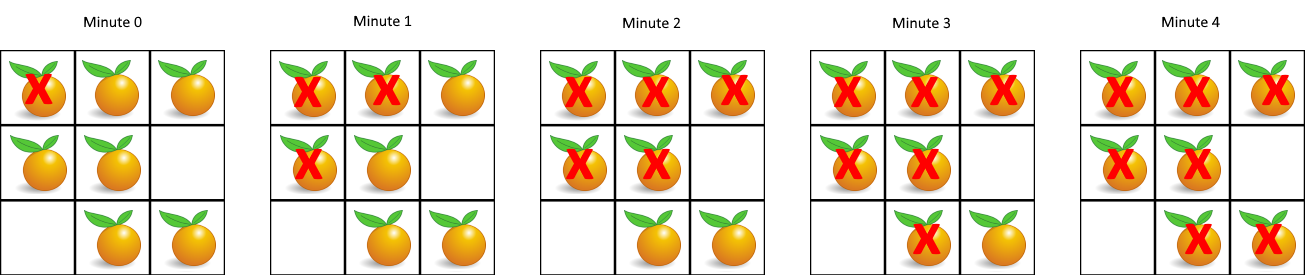
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4
Example 2:
Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
Example 3:
Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 10grid[i][j]is0,1, or2.
Solution
Since we are asked to find the when we will reach the final stage of the oranges, we must find the final stage first. Each minute, the rotten oranges will rot its neighboring oranges, thus the best way to approach this question is BFS starting with the rotten oranges, each minute we expand the breadth by 1 layer. We keep a counter of the minutes passed, and in the very end check whether all oranges are rotten.
We will follow these steps to implement this problem.
- put all rotten oranges into a queue
- BFS on queue to rot other oranges,
minutes= number of levels in BFS - check whether there are unrotten oranges (return -1)
def orangesRotting(grid: List[List[int]]) -> int:
m = len(grid)
n = len(grid[0])
minute = -1
rot = deque()
has_orange = False # whether grid contain an orange
for x in range(m):
for y in range(n):
has_orange = has_orange or grid[x][y]
if grid[x][y] == 2: # rotten orange
rot.append((x, y))
if not has_orange: return 0 # no orange in grid, return 0
while rot: # bfs to rot oranges
minute += 1
count = len(rot)
for _ in range(count):
x, y = rot.popleft()
if x+1 < m and grid[x+1][y] == 1:
grid[x+1][y] = 2
rot.append((x+1, y))
if x-1 >= 0 and grid[x-1][y] == 1:
grid[x-1][y] = 2
rot.append((x-1, y))
if y+1 < n and grid[x][y+1] == 1:
grid[x][y+1] = 2
rot.append((x, y+1))
if y-1 >= 0 and grid[x][y-1] == 1:
grid[x][y-1] = 2
rot.append((x, y-1))
for x in range(m): # check for unrotten oranges
for y in range(n):
if grid[x][y] == 1:
return -1
return minute
Ready to land your dream job?
Unlock your dream job with a 2-minute evaluator for a personalized learning plan!
Start EvaluatorHow would you design a stack which has a function min that returns the minimum element in the stack, in addition to push and pop? All push, pop, min should have running time O(1).
Recommended Readings
LeetCode Patterns Your Personal Dijkstra's Algorithm to Landing Your Dream Job The goal of AlgoMonster is to help you get a job in the shortest amount of time possible in a data driven way We compiled datasets of tech interview problems and broke them down by patterns This way we
Recursion Recursion is one of the most important concepts in computer science Simply speaking recursion is the process of a function calling itself Using a real life analogy imagine a scenario where you invite your friends to lunch https algomonster s3 us east 2 amazonaws com recursion jpg You first
Runtime Overview When learning about algorithms and data structures you'll frequently encounter the term time complexity This concept is fundamental in computer science and offers insights into how long an algorithm takes to complete given a certain input size What is Time Complexity Time complexity represents the amount of time
Want a Structured Path to Master System Design Too? Don’t Miss This!